发表更新算法19 分钟读完 (大约2917个字)0次访问

分治策略&动态规划

这期我从分治策略和动态规划两个角度出发来比较两种算法的异同点，同时分析常见的递归优化方案，包括记忆化搜索和尾递归， 然后引出动态规划是解决某些问题的最优方法。

概念

开始前先介绍几个概念：

  • 自顶向下，理解为从问题的终点向问题的起点解决
  • 自底向上，理解为从问题的起点向问题的终点解决
  • 最优子结构：当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质
  • 重叠子问题：在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次

分治策略

如果原问题可分割成k个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。

由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。

在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。

分治算法通常使用递归的方式来求解

特征：

  • 规模如果很小，则很容易解决。

  • 大问题可以分为若干规模小的相同问题。//即要求具有最优子结构性质

  • 利用子问题的解，可以合并成该问题的解。

  • 分解出的各个子问题相互独立，子问题不再包含公共子问题。 //不一定需要满足，可以有重叠

经典的分治递归例子：斐波那契数列

看结构：

  1. 满足规模小，容易解决 -> 1+1=2 1+2=3
  2. 满足最优子结构，具体看图
  3. 满足子问题的解可合成该问题的解
  4. 子问题有重复，不影响分治算法的使用，但是会影响效率

一般的递归写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 一般递归写法

let count = 0;

const fib = (n) => {
  console.trace()
  count++;
  if(n === 0 || n === 1){
    return 1;
  }
  return fib(n-1) + fib(n - 2);
};

console.time("time");
let res = fib(30);
console.timeEnd("time");

console.log('res:', res, 'count:', count);

这种方法的优势在于每一步都看得很明白，对于斐波那契数列的结构也很清晰，但不好的地方在于，时间复杂度非常高，达到指数级，只要n变大，就出现爆栈和超时的问题。

时间复杂度：
O(2^n) (渐进上界)
O(1.618^n) (紧渐进界 具体推演过程)

空间复杂度：O(1)

优化方式一：记忆化搜索

在原本的斐波那契递归中，总会像如上图一样递归到最后再返回结果

其中，例如 以5为例，3往下的部分，就会被重复计算两次，2往下的部分会被重复计算3次。

我们使用memo来缓存每一次的结果，下次如果再解决同样的子问题，就可以直接拿来使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//记忆化搜索

let count = 0;
let memo = [];

const fib_memo = (n) => {
  console.trace()
  count++;
  if(n === 0 || n === 1){
    return 1;
  }
  if(!memo[n]){
    memo[n] = fib_memo(n-1) + fib_memo(n - 2)
  }
  return memo[n];
};

console.time('time');
let res = fib_memo(10);
console.timeEnd('time')

console.log('res:', res, 'count:', count);

时间复杂度：O(n)

空间复杂度：O(n)

虽然时间复杂度度大大降低了，但这仍然影响性能。

因为在程序调用一个函数时，栈中会分配一块空间来保存与这个调用相关的信息，每一个调用都会被当作是活跃的。栈上的那块存储空间称为活跃记录或者栈帧。

然后因为递归函数在调用的时候会不断的创建一个栈帧来保存上一个函数的调用信息，栈上的栈帧越来越多，就会导致爆栈 Maximum call stack size exceeded。

接下来的目的就是去优化函数的调用栈，下面介绍尾递归。

优化方式二：尾递归

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归的

下面几种情况都不是尾递归：

1
2
3
4
5
6
7
8
9
10
11
12
function fn() {  
  return gn() + 10//调用之后又赋值
}

function fn() {  
  gn()//没有return，或者说是return了undefined
}

function fn() {  
  let gnn = gn();  
  return gnn//调用后还有操作
}

当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。

编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。

通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 尾递归

let count = 0;

const fib_tail = (n, num = 1, sum = 1) => {
  console.trace()
  count++;
  if (n<=1){
    return sum;
  }
  return fib_tail(n-1, sum, num + sum);
}

console.time('time');
let res = fib_tail(10);
console.timeEnd('time')

console.log('res:', res, 'count:', count);

时间复杂度： O(n)
空间复杂度： O(1)

可以看到此时这个算法的效率已经非常高了，但这仍然不是最优解，因为存在函数的调用开销，下面开始介绍动态规划算法。

动态规划算法

动态规划算法（Dynamic Programming）与分治算法相似，都是通过组合子问题的解来求解原问题的解。

但是两者之间也有很大区别：分治法将问题划分为互不相交的子问题，递归的求解子问题，再将他们的解组合起来求解原问题的解；与之相反，动态规划应用于子问题相互重叠的情况，在这种情况下，分治法还是会做很多重复的不必要的工作，他会反复求解那些公共的子问题，而动态规划算法则对相同的每个子问题只会求解一次，将其结果保存起来，避免一些不必要的计算工作

特征

  • 大问题可以分为若干规模小的相同问题。//即要求具有最优子结构性质

  • 子问题空间必须足够” 小 “，也就是说原问题递归求解时会重复相同的子问题，而不是一直生成新的子问题。 //即有重叠子问题

思考步骤：

  1. 划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。(划分子问题)

  2. 确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。(状态表示)

  3. 确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。（子问题与下个子问题间的关系式）

  4. 寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。（边界条件）

比如斐波那契数列：1 1 2 3 5 8 13 21 … ，求第n项的值

第一步：输入1，输出1；输入2，输出1；输入3，输出2，通过分析可知道第n项值等于第n-1和n-2项的和

第二步：最后一项为f(n)，两项分别为f(n-1)、f(n-2)

第三步：状态转移方程：dp(n) = dp(n-1) + dp(n-2)

第四步：边界条件为dp[1]=1, dp[2]=1 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 不带缓存的dp

let count = 0;

const fib_dp_unmemo = (n) => {
  let dp = [];
  dp[0] = 0;
  dp[1] = 1;
  for(let i = 2; i <= n; i++) {
    count++;
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
}

console.time('time')
let res = fib_dp_unmemo(30)
console.timeEnd('time')

console.log('res:', res, 'count:', count);

此时时间复杂度为O(n), 空间复杂度为O(n)，这还不够优雅，因为空间消耗的也多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 带缓存的dp

const fib_dp_memo = (n) => {
  let front = 0;
  let back = 1;
  let res = 0;
  for(let i = 2; i <= n; i++) {
    res = front + back;
    front = back;
    back = res;
  }
  return res;
};

let res = fib_dp_memo(30);

使用变量保存下一次循环需要的子问题结果，而不是保存全部结果，这样能大大减少内存

此时时间复杂度为O(n), 空间复杂度为O(1)

动态规划对比于尾递归，通过一次迭代得到结果，函数的调用开销减少了，同时时空间复杂度和尾递归相同，是解决这个问题的最优解！

拓展

leetcode 题号：198.打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，

如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 400

首先考虑最简单的情况。如果只有一间房屋，则偷窃该房屋，可以偷窃到最高总金额。

如果只有两间房屋，则由于两间房屋相邻，不能同时偷窃，只能偷窃其中的一间房屋，因此选择其中金额较高的房屋进行偷窃，可以偷窃到最高总金额。

如果房屋数量大于两间，应该如何计算能够偷窃到的最高总金额呢？

对于第 k (k>2) 间房屋，有两个选项：

  1. 偷窃第 k 间房屋，那么就不能偷窃第 k-1 间房屋，偷窃总金额为前 k-2 间房屋的最高总金额与第 k 间房屋的金额之和。

  2. 不偷窃第 k 间房屋，偷窃总金额为前 k-1 间房屋的最高总金额。

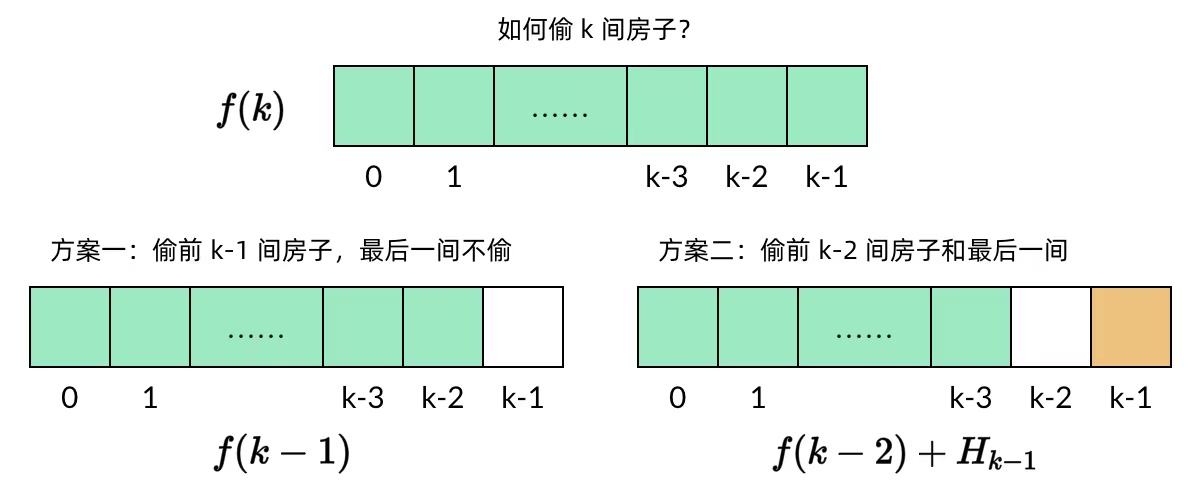
在两个选项中选择偷窃总金额较大的选项，该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。

用 dp[i] 表示前 i 间房屋能偷窃到的最高总金额，那么就有如下的状态转移方程：

dp[i] = max(dp[i−2] + nums[i], dp[i−1])

边界条件为：
dp[0] = nums[0] //只有一间房屋，则偷窃该房屋
dp[1] = max(nums[0], nums[1]) //只有两间房屋，选择其中金额较高的房屋进行偷窃

1
2
3
4
5
6
7
8
9
10
11
12
13
const rob = (nums) => {
    const len = nums.length;
    if(len == 0){
      return 0;
    }
    const dp = new Array(len + 1);
    dp[0] = 0;
    dp[1] = nums[0];
    for(let i = 2; i <= len; i++) {
      dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
    }
    return dp[len];
};

还不够，进行空间优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const rob = (nums) => {
    const len = nums.length;
    if(len == 0){
      return 0;
    }
    let front = 0;
    let back = nums[0];
    let res = 0;
    for(let i = 2; i <= len; i++) {
      res = Math.max(back, front + nums[i-1]);
      front = back;
    	back = res;
    }
    return res;
};

评论

目录

归档

分类

最新文章

×